高中数学立体几何题型丰富多样，涵盖了作图、证明、求值等多个方面。踏入立体几何的世界，需精通基础概念，如线面平行垂直判定，巧用空间向量破解难题。掌握题型大全，总结做题技巧，让空间想象跃然纸上，逻辑推理严谨有序，成就数学高手之路。以下是对高中数学立体几何题型大全及做题技巧的总结：

高中数学立体几何题型丰富多样，涵盖了作图、证明、求值等多个方面。以下是对高中数学立体几何题型大全及做题技巧的总结：

注：完整版《高中数学立体几何题型大全及做题技巧总结》在文章末尾下载

题型大全

作图题型

1. 作交集：包括线线交点、线面交点、面面交线的作图。
2. 作平行：涉及线线平行、线面平行、面面平行的作图。
3. 作垂直：包括线线垂直、线面垂直、面面垂直的作图。

证明题型

1. 证隶属：如点点重合、点在线上、点在面上等。
2. 证平行：
3. 线线平行：通常利用平行线的性质或平行四边形的性质进行证明。
4. 线面平行：常用方法包括利用线面平行的判定定理、构造平行四边形、作辅助面等。
5. 面面平行：依据判定定理，证明一个面内两条相交直线与另一个平面平行。
6. 证垂直：
7. 线线垂直：利用直角、垂直线的性质或三垂线定理等。
8. 线面垂直：证明直线与平面内两条相交直线垂直。
9. 面面垂直：证明一个平面内两条相交直线与另一个平面垂直。

求值题型

1. 求距离：包括点点距、点线距、点面距、线线距、线面距、面面距等。常用方法有向量法、等面积法、三棱锥体积法等。
2. 求角度：涉及线线角、线面角、面面角的求解。常用向量夹角公式或三垂线定理进行求解。
3. 综合题型
4. 命题判断：给出几个关于立体几何直线与平面位置关系的命题，要求判断其真伪。
5. 几何体体积与表面积计算：包括旋转体、椎体、柱体或其组合体的体积或表面积计算。
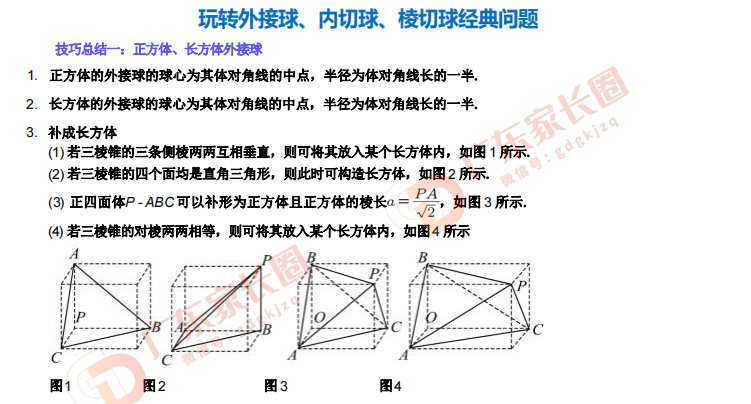
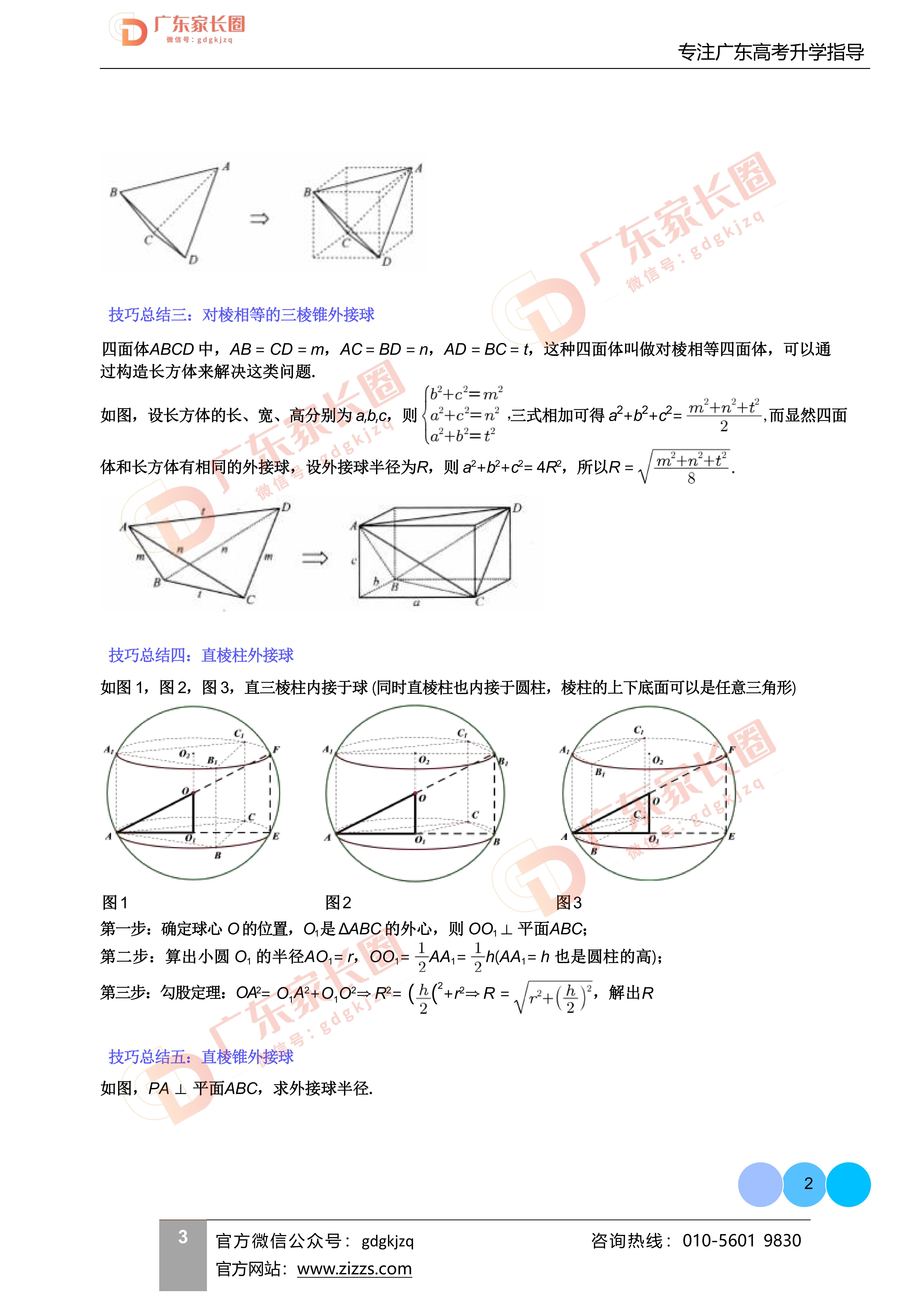
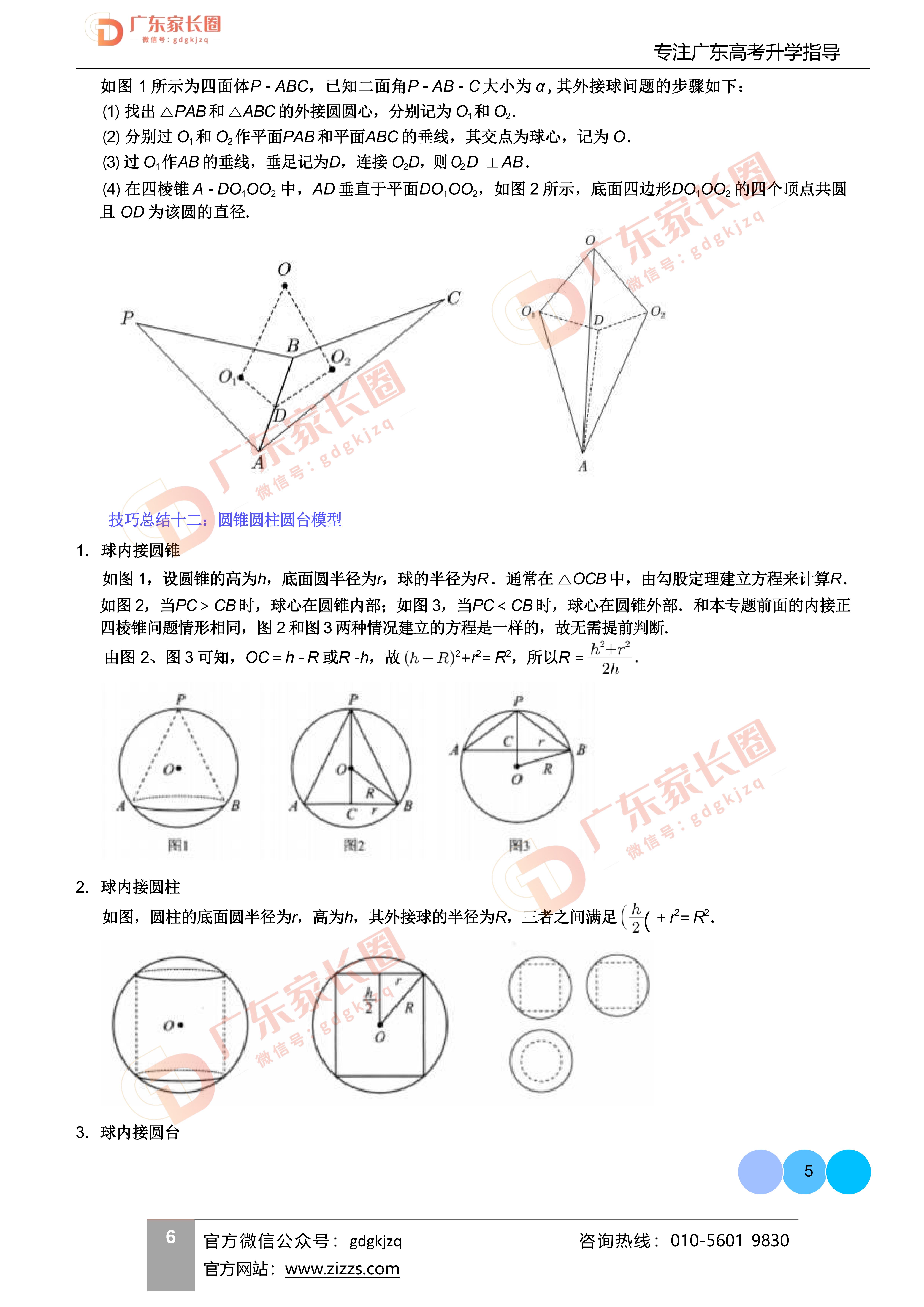
6. 与球有关的问题：如球的内外切问题、外接球问题等。

做题技巧

1. 分析法与综合法相结合：由已知想性质，由求证想判定，寻找证题思路。
2. 适当添加辅助线（或面）：利用题设条件的性质适当添加辅助线或面，是解题的常用方法之一。
3. 掌握基本定理和性质：如线面平行的判定定理、线面垂直的判定定理等，这些定理和性质是解题的基础。
4. 灵活运用向量法：向量法在立体几何中的应用非常广泛，可以用于证明平行、垂直关系，以及求解距离和角度等问题。掌握向量的基本概念和运算规则是运用向量法的关键。
5. 注意空间想象能力的培养：立体几何问题需要较强的空间想象能力，平时可以通过观察实际物体、绘制立体图形等方式来培养这种能力。
6. 总结归纳题型和解题方法：在学习过程中，要注意总结归纳常见的题型和解题方法，形成自己的解题思路和技巧体系。

通过以上对高中数学立体几何题型大全及做题技巧的总结，希望能对同学们的学习有所帮助。